前言
在上一节课中我们讨论过确定性时间复杂度,以及时间层谱定理,还介绍了两个复杂度类:P和EXP。这节课我们将会介绍另外一个复杂度类,叫做NP,并且学习它于P和EXP的关系。此外,我们将会定义一个改版的多项式时间的映射约化,再加一个NP类的完全性概念。
备注20.1. NP-完全性的概念是目前计算机科学对当今科学界最重要的贡献之一;NP-完全性问题,非常著名,在整个数理科学中随处可见。因此本书有必要提及这个概念。
然而在滑铁卢大学中,复杂度类NP和NP完全性概念,包含在一个不同的课程中,CS 341 Algorithm。由于这个原因,我们在本课程中没有着重讲解 — 这里我们只当NP类是一个重要的复杂度类案例。特别是,我们将不会提及证明某个语言是NP-完全性的证明技术,但是那些刚接触这个课题的人可以放心,有成千上万个有趣的案例,包括一些具有重要现实意义的例子,都是已知的。
知识点
复杂度类NP
可以从两个角度来理解复杂度类NP,一个是NP这个名称,它是那些可以在非确定性多项式时间内判定的语言所组成的类。另一个就更直观也更好应用,它是可以在多项式时间内验证的的语言所组成的类,给出这个语言中任意字符串对于所求问题的多项式长度的证书(certificate)。
NP作为多项式时间的非确定性计算
正如我们上面说到的,我们可以通过NP类的名称来做定义,也就是非确定性多项式时间
开始之前,我们先明确一个非确定性图灵机的运行时有什么意义。
定义20.2. 已知$N$是一个NTM,它的输入字母表是$\Sigma$。对于每个输入字符串$w\in\Sigma^{*}$,让$T(w)$表示$N$执行$w$最大步数,考虑所有可能的非确定行计算路径。$N$的运行时函数$t:\mathbb{N}\rightarrow\mathbb{N}\cup\{\infty\}$的定义如下
其中每个$n\in\mathbb{N}$。用文字表达,对于所有长度为$n$的输入字符串及其在$N$中全部非确定性选择,$t(n)$是$N$停止所需的最大步数。
和我们上节课中一样,我们要先定NTM对于所有长度的输入的运行时都是有限的。
让我们回想第18课中非确定性图灵机的判定性是怎么表示的:一个NTM $N$能判定一个语言$A$的条件是$A=L(N)$并且$N$对于每个输入都存在一个有限的计算树。这样,如果$N$是一个NTM,它的运行时是$t$,$w$是一个$N$的输入字符串,$N$输入$w$的的计算树的深度边界是$t(|w|)$。这个成为一个可接受计算条件是它至少存在一个接受配置,否则,如果整个树中都没有接受配置, 那他就是一个拒绝计算。
我们现在可以定义NTIME$(f)$,对于每个函数$f:\mathbb{N}\rightarrow\mathbb{N}$,作为所有能被非确定性图灵机判定语言的复杂度类,运行时为$O(f(n))$。这样定义NTIME$(f)$之后,我们像定义P那样来定义NP:
NP作为证书校验
第二种看待NP的方式是作为一个可以在多项式时间内验证的语言类,已知一个多项式长度的从属关系证书。我们将要声明一个定理,这个概念将等价于复杂度类NP的从属关系,正如(20.2)定义。
然而在我们声明这个定理之前,让我们引入一个简单的术语。往后,一个形如:$p:\mathbb{N}\rightarrow\mathbb{N}$的函数是一个多项式界限函数的条件是它是时间可构建的并且对于某个正整数$k$满足$p(n)=O(n^k)$。
定理20.3. 已知$\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个语言。语言$A$包含于NP当且仅当存在一个多项式界限函数$p$和一个语言$B\in P$使得
关于这个定理的解释是字符串$y$扮演了验证或者证明字符串$x$包含于$A$的角色,同时语言$B$代表着一个有效的验证程序,检测$x$关系证明的有效性。术语证据(witness)是证书的另外一个称呼。
证明这个定理需要验证如下两层含义,我们不做详细讲解。
- 已知一个语言$A$如定理中等式(20.3)中所描述,我们可以得出$A\in NP$,通过定义一个多项式时间的NTP $N$,那么它可以非确定性地猜测一个二进制字符串$y$,长度最多为$p(|x|)$,并且判定关系$\langle x,y\rangle$属于$B$。
- 如果$A\in NP$,那么我们可以找到一个可以判定$A$的多项式时间的NTM $N$,我们可以将$N$输入$x$的每个非确定性计算的路径编码某个二进制字符串$y$,它的长度不超过$p(|x|)$,$p$是某个多项式界限函数。然后我们定义$B$是一个可以在多项式时间内判定字符串$\langle x,y\rangle$的语言。
P、NP和EXP的关系
现在让我们观察下面这个包含关系:
第一个包含关系,$P\subseteq NP$,是很明显的。每个DTM都有一个与之等价的没有非确定性选择的NTM,所以
其中所有函数形式为$f:\mathbb{N}\rightarrow\mathbb{N}$。这表示
其中所有$k\geq 1$,因此$P\subseteq NP$。
或者,根据定理20.3中NP的描述,假设$A\subseteq\Sigma^{*}$是一个基于字母表$\Sigma$的语言,并且$A\in P$。那么我们可以定义一个语言$B$如下:
很显然$B\in P$;只要$A$是多项式时间内可判定的,我们也可以轻松在多项式时间内判定$B$。对于任意多项式界限函数$P$,定理(20.3)的情况是满足的,因此$A\in NP$。
现在让我们看看$NP\subseteq EXP$。假设$A\subseteq\Sigma^{*}$是一个基于字母表$\Sigma$的语言,并且$A\in NP$。根据定理20.3,存在一个多项式界限的函数$p$和一个语言$B\in P$使得定理(20.3)有效。定义一个DTM $M$如图20.1所示。显然$M$能够判定$A$,它只需要搜索所有二进制字符串$y$的集合,$|y|\leq p(|y|)$,看是否存在一个字符串使得$\langle x,y\rangle\in B$。
剩下的就是考虑$M$的运行时,让我们先观察第2步,其中$M$检测$\langle x,y\rangle\in B$,输入字符串$x\in\Sigma^{*}$,还有$y$满足$|y|\leq p(|x|)$。这个检测的步数是$|x|$的多项式级时间,原因如下。首先,我们有$|y|\leq p(|x|)$,因此字符串$\langle x,y\rangle$的长度是多项式界限的。现在,因为$B\in P$,我们可以在多项式时间内确定从属于$B$这个关系。因为输入是$\langle x,y\rangle$,这表示检测从属于$B$的时间是$|\langle x,y\rangle|$的多项式级。然而,因为两个多项式界限函数的复合还是多项式界限的,我们发现检测是否$\langle x,y\rangle\in B$的时间是$x$的多项式级。第3步也能$x$的多项式时间内执行完,同样第4步也可以。
最后,再次假设$f$是一个多项式界限函数,那么$f(n)=O(n^k)$,其中$k$是正整数,我们发现刚才所讨论的步骤总共需要执行的步数做多是
使用上界模糊处理,每个多项式界限函数$g$,满足$g(n)=O(2^n)$,我们发现整个$M$的计算运行时是
我们已构建出$M$的运行时是指数级时间的,所以$A\in EXP$。
现在我们知道
而且我们也知道
根据时间层谱定理。当然这表示两个真包含关系:(i)$P\subsetneq NP$,和(ii)$NP\subsetneq EXP$中有一个或者两个都满足。但是至今都还没有证明,任意一个正确的证明都能为复杂度理论带来突破性进展。的确,判定是否$P=NP$被认为是当今数学领域最重要的未解决问题之一。
多项式时间约化和NP-完全性
在第17节课中我们讨论过约化,并且使用它来证明特定语言的不可判定性和非半可判定性。多项式时间约化的定义也是类似的,除了一个限定条件:约化必须由一个多项式时间的可计算函数得出。
定义20.4. 已知$\Sigma$和$\Gamma$是字母表,$A\subseteq\Sigma^{*}$和$B\subseteq\Gamma^{*}$是语言。我们说$A$能够多项式时间约化成$B$的条件是存在一个多项式时间的可计算函数$f:\Sigma^{*}\rightarrow\Gamma^{*}$使得
其中所有$w\in\Sigma^{*}$。我们写作
来表示$A$能够多项式约化成$B$,并且任意构造这个关系的函数$f$被我们成为$A$到$B$的多项式时间约化。
有时候我们又把多项式时间约化称作多项式时间映射约化(或者多项式时间多一约化)来区别于其他类型的约化 — 但是这里我们简单一点就叫它多项式时间约化即可。有时候我们也称它为卡普约化(Karp reduction),得名于Richard Karp,一个NP-完全性理论的先驱。
有了多项式时间约化的定义在手,我们现在就能定义NP-完全性了。
定义20.5. 已知$\Sigma$是一个字母表,$B\subseteq\Sigma^{*}$是一个语言。
- 我们说$B$是NP-困难的条件是对于每个语言$A\in NP$存在关系$A\leq^p_m B$。
- 我们说$B$是NP-完全的条件是$B$是NP-困难并且$B\in NP$。
这个定义背后的想法是NP-完全语言代表着NP中最难判定的语言;每个NP中的语言都能在多项式时间约化成一个NP-完全语言,所以如果我们忽略执行一个多项式时间约化的难度,那么判定任意一个NP-完全语言都能降低整个NP类的计算难度。图20.2说明了类P、NP、NP-困难和NP-完全语言的关系,假设了$P\neq NP$。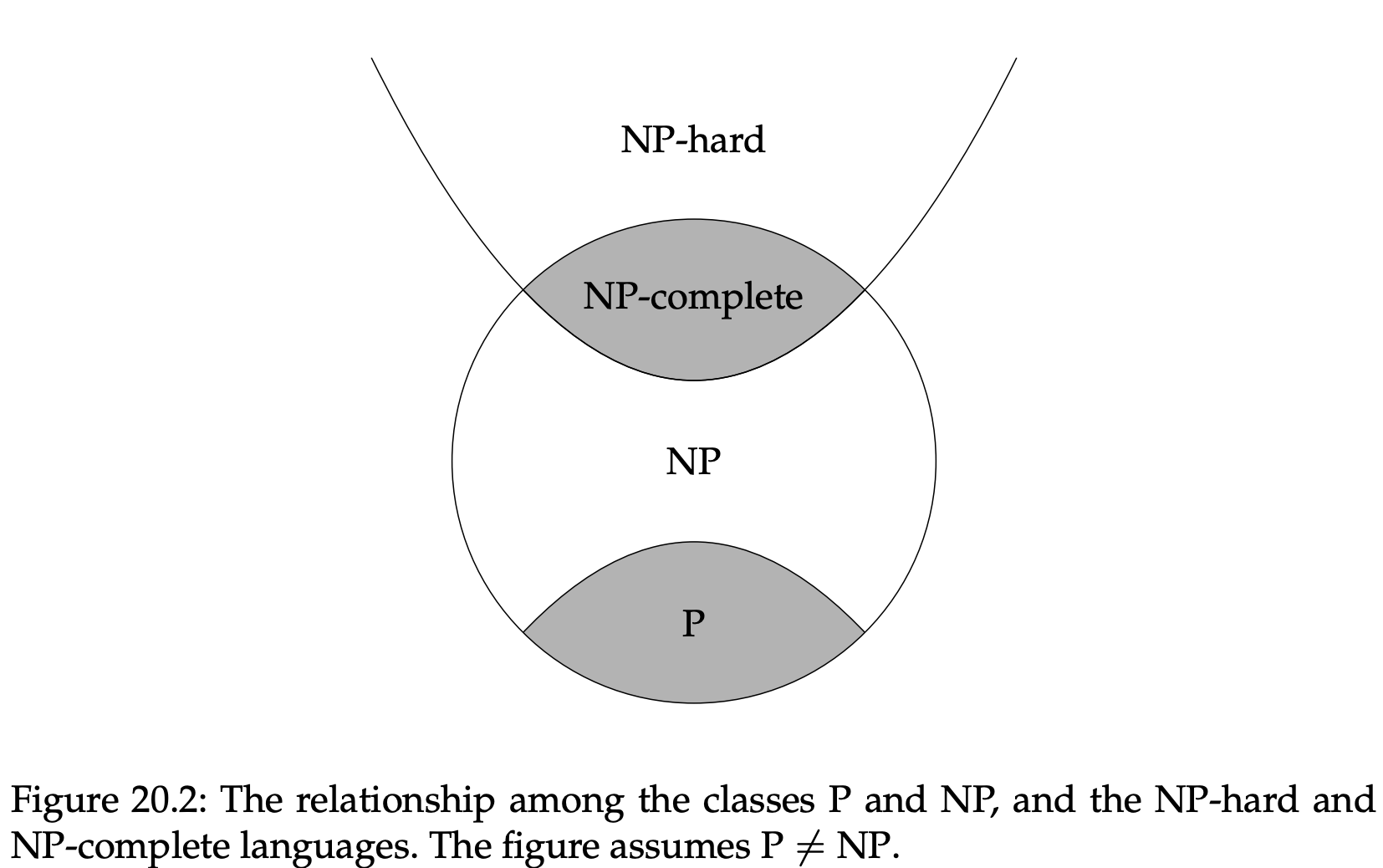
这里有一些关于多项式时间约化和NP的基本事实。这些所有的事实都基于假设A、B和C的字母表是任意的。
- 如果$A\leq^p_m B$并且$B\leq^p_m C$,那么$A\leq^p_m C$。
- 如果$A\leq^p_m B$并且$B\in P$,那么$A\in P$。
- 如果$A\leq^p_m B$并且$B\in NP$,那么$A\in NP$。
- 如果$A\leq^p_m B$并且$A$是NP-困难的,那么$B$也是NP-困难的。
- 如果$A\leq^p_m B$,$A$是NP-完全的并且$B\in NP$,那么$B$是NP-完全的。
- 如果$A\in P$并且$A$是NP-困难的,那么$P=NP$。
通常我们使用第5条声明来证明某个特定的语言$B$是NP-完全的:首先我们证明$B\in NP$(通常比较简单),然后找到一个已知的NP-完全语言$A$,我们来证明$A\leq^p_m B$。
这条声明的证明就是上面所说这么直接,有兴趣你们可以自己证明。这里我们就只选取一条声明来证明。
命题20.6. 已知$A\in\Sigma^{*}$和$B\in\Gamma^{*}$是语言,其中$\Sigma$和$\Gamma$是字母表,假设$A\leq^p_m B$并且$B\in NP$。那么情况是这样$A\in NP$。
证明:让我们把关于这个命题所有假设的细节汇集起来。
首先因为$A\leq^p_m B$,我们知道一定存在一个多项式时间的可计算函数$f:\Sigma^{*}\rightarrow\Gamma^{*}$使得
其中所有$x\in\Sigma^{*}$。因为$f$是一个多项式时间内可计算的,一定存在一个多项式界限函数$p$使得$|f(x)|\leq p(|x|)$,对于所有$x\in\Sigma^{*}$。
然后,根据假设$B\in NP$,一定存在一个多项式界限函数$q$和一个语言$C\in P$满足
现在,我们定义一个新的语言
很明显$D\in P$,因为我们可以轻松地在多项式时间内通过$\langle x,y\rangle$得出$\langle x,y\rangle$(已知$f$是多项式时间内可计算的),然后检验是否$\langle f(x),y\rangle\in C$,这个过程也是多项式时间的,因为$C\in P$。
最后,观察一下
因为复合函数$q\circ p$是多项式界限的,并且$D\in P$,也就是说$A\in NP$。
本节课我们得出了下面这个推论,它是上一个命题跟时间层谱定理结合的有趣应用。
推论20.7. $NP\neq DTIME(2^n)$.
证明:使用反证法假设$NP=DTIME(2^n)$。让$\Sigma$作为任意一个字母表,$A\subseteq\Sigma^{*}$是一个任意属于$DTIME(4^n)$的语言,然后定义

首先我们观察到$B\in DTIME(2^n)$。具体一点,图20.3中的DTM $M$可以在时间$O(2^n)$之内判定$B$。$M$运行时为$O(2^n)$的理由是:第一步能轻松在多项式时间内完成,第二步需要步骤数是$O(4^{n/2})=O(2^n)$,因为$A$对于输入长度$m$能在时间$O(4^m)$内判定,并且这里我们判定关系在$A$中的字符串长度是$m=n/2$。因此$M$的运行时是$O(2^n)$。因为我们假设了$NP=DTIME(2^n)$,也就是说$B\in NP$。
现在我们定义一个函数$f:\Sigma^{*}\rightarrow\Sigma^{*}$为
其中所有$x\in\Sigma^{*}$。函数$f$能够在多项式时间内计算,通过$B$的定义我们得出
因此我们得到了$A\leq^p_m B$。根据命题20.6,得出$A\in NP$,而且已知假设$NP=DTIME(2^n)$,也就是说$A\in DTIME(2^n)$。
然而,因为$A$是一个任意选取属于$DTIME(4^n)$的语言,我们得出$DTIME(4^n)\subseteq DTIME(2^n)$。这就和时间层谱定理矛盾了,所以假设$NP=DTIME(2^n)$是错误的。